Clock flowers in Year 4

In the course of our counting circle sessions we looked at clock counting (mod 60 counting).

We took this a bit further. using a Scratch project to generate these easily. 

It was a great opportunity for mathematical noticing, reasoning and claim-making. For instance

1. 
   Rose15 December 2014 at 02:33

   The odd numbers go to every stop
   
   
   

   1. 
      Justus15 December 2014 at 02:38

      I do not think so, because 15 is a odd number and it does not meet every stop

and

Justus15 December 2014

I notice that all of the prime number under 22 meet all of the numbers under 59 on the clock.It looks so cool!

1. 
   Mr Grgg15 December 2014

   What you say is almost true, Justus, but what about 2, 3 and 5?
   
   What do you think?
2. 
   Justus16 December 2014

   3 5 7 do not visit all of the numbers because are the factors of 60

The class also had a go at creating some of the "clock flowers" by hand:

and looked at the same thing in terms of division:

There's a lot more mileage in these clock patterns. Who knows where we'll take it next time... maybe string patterns?

Fairground Games

Year 9 have completed their annual probability project where they design, test and run a ‘fairground’ for visiting year 6 students. It is always great fun and this year was no exception. The exercise is all about experimental probabilities. By designing games carefully, you should be able to predict that more people will lose a game than win it. With theoretical games, you can calculate it. The challenge is to make a game that people want to play, that is possible to win, but that people are mostly likely to lose so the stall holder wins in the end. So it is great to put these games to real test. Year 6 obliged and were very discerning with their money. Some of them went home with more than they came with, but on balance the fairground won - just. This years winners were Nicholas and Kieran whose brave ‘wet sponge throw’ (it was cold outside) won the most money. A direct hit in the face was required to win, but apparently the punters felt a body hit was worth the cost! Great design and aesthetics from the ‘Jungle challenge’ and ‘jungle hoops’ and lots of terrific ideas involving everything from Nerf guns and roulette wheels! A terrific event - well done to all who took part! 

Counting Circles in Year 4

We've been trying out "Counting Circles" in Year 4, and it's starting to get into its stride. Obviously there are lots of ways to count, but we've begun to do it in a very particular way (here described by John Golden, based on Sadie Estrella's lessons). This, for us, involves sitting in a circle, and counting from a chosen number in a certain-sized jump. On the first day we started from zero and jumped up in twos, with the teacher writing down the steps on the whiteboard.

Day 1

Easy enough. Then at a certain point (52 on the first day) we stop and the teacher says:

"What number would Marie (for example) be who's three people after 52? Think about it and put your hand up when you've come up with an answer." 

Then the good bit comes: the explanation. "Who could share the way they worked out that it was 58?"

Usually there are a number of explanations, and a number of ways of getting to the answer. Children explain their thinking, and we note it down on the whiteboard.

Day 2

Day 3

Day 4

Day 5

We've been doing this for perhaps five or ten minutes at the start of some of our lessons, then we leave it and go onto something else. 

This last week we've been looking at time on the analogue clock, so it made sense to do a bit of clock counting, following the way the minutes go ("counting in mod 60"):

Day 9: Clock counting

(Apologies - very shaky video!)

The next day was clock counting with jumps of eight (it took two times round the clock to get back to zero).

The day after, jumps of eleven:

Day 11

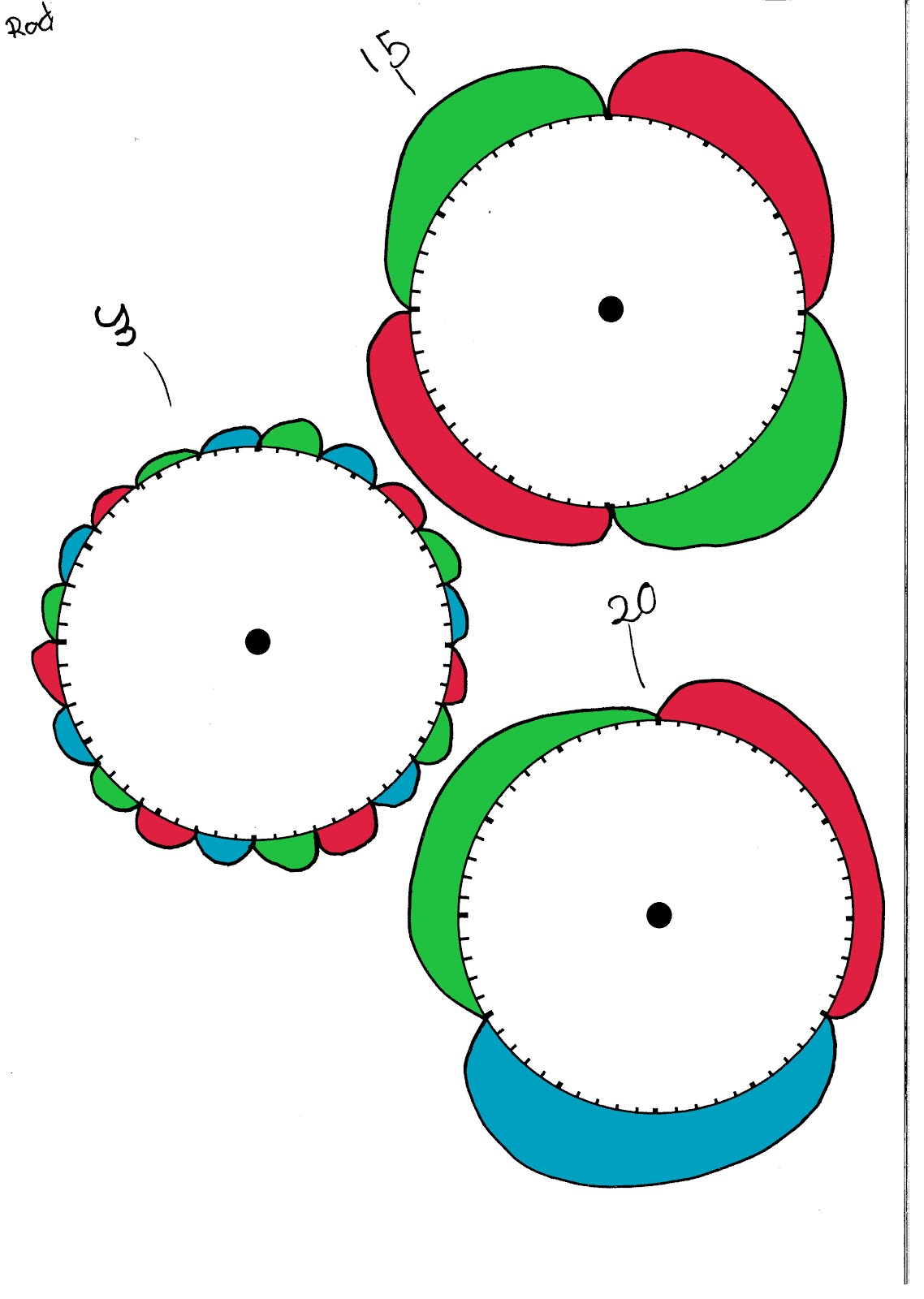
There were lots of great ways of getting the person three jumps on's number. James was looking at the vertical pattern all the way across. Alya spotted a diagonal pattern. Rod added three to each digit, rembering that the 6 for sixty became zero. And Samyak added 33 and knew that 68 is actually just 8 in clock counting.

It's early days yet. It's been a good moment for us to share our reasoning and see that we often know more than one good method. We'll keep going with it. We'll try new jumps, and also work on not correcting each other's mistakes, and at listening to each other's explanations really carefully.

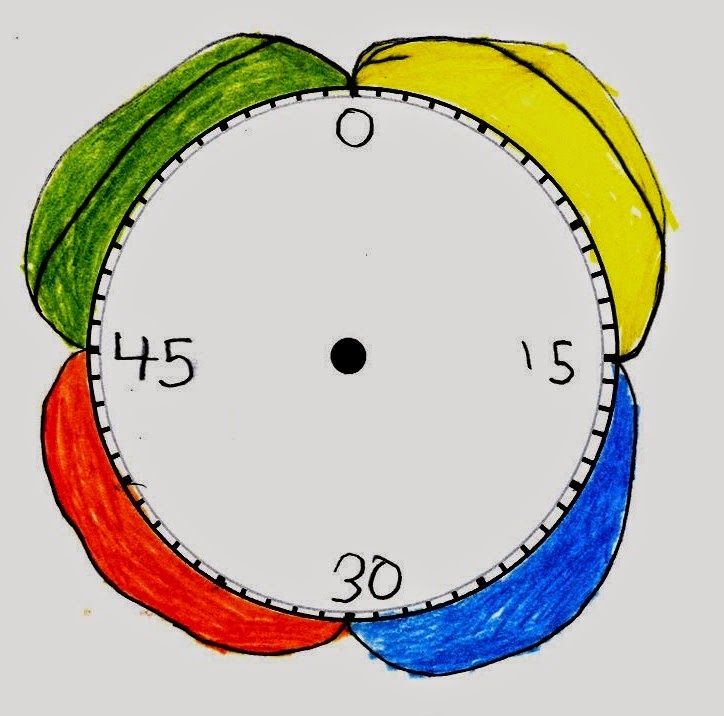
PS. See the Year 4 blog to see how we later continued with the clock counting patterns on paper to create Clock Flowers.

Seeing through these problems

At our school in Toulouse, the classrooms have one wall that is almost entirely glass and big double glass doors on the opposite wall. This makes for a lovely light a spacious room but sometimes leaves us short of wall space! Imagine then my delight and discovering 'Window Markers!' My classroom walls are now becoming adorned with lovely maths problems! Here are a couple of problems that are on the door at the moment....

Can you solve the problem on the door of P5? #istlive pic.twitter.com/HnHkSMub8J
— Mr Noble (@MathsinP5) November 18, 2014

I am sure many have seen this problem before, but Mathematics is never going to run out of things for us to spend more time looking at. I picked this up from a friend's daughter's homework they were asking me about. The problem has a couple of particular fascinations for me based on playing with it myself and putting it on my classroom door.

1. That there are some quite different ways to approach it
2. That there is significance difference between asking students or a particular unknown length and a more general 'given the diagram, what else can you tell me that is true?' approach

That last thought has occupied me for a while....

Here is another one!

Another problem on the door of P5 #istlive pic.twitter.com/W5J9nblp1U

— Mr Noble (@MathsinP5) November 19, 2014

This took even more thought! and even prompted +Simon Gregg to write this blog post when he first saw it!

No solutions here as that would spoil the fun!

Estimation challenges

Children in Year 4 have had a piece of homework: devise an estimation challenge for the rest of Year 4. You can see the great challenges by clicking here. They've also been trying to answer each others' questions.

This came after we've spent a fair bit of time on Andrew Stadel's great site estimation180.com, recording our upper and lower limits and estimation on the Google docs for some of the challenges. There's something really engaging about being presented with these mystery quantities, amounts, numbers and measurements, and trying to zero in on a reasonably accurate answer.

The Year 4 students produced a real variety of challenges: measuring ones like how tall is Milly, the world's smallest dog?

Ones involving part of a known quantity, like how many matches are left in the matchbox?

And lots of counting challenges, including some where you need to sample part of the picture and then scale it up to account for the whole picture, like Hama bead estimation.

It's really great how families have helped with this, with the maths, and with filming and photographing, and also how everyone has been able to write their post, upload their pictures that give clues and also links or videos that reveal the answer. And of course the estimates in the comments have been great too! If you'd like to have a go, please do. No peeking though!

Patterns of cubes - the first in the sequence

Looking at patterns and how they grow is something we've done lots before. But this time in Year 4 we took particular time over something different: what exactly the first step should be.

Look at this pattern here, a pattern of "C" shapes:

We had a long discussion about that first single cube. Did it really belong in the sequence? Some thought yes, some no. We didn't really come to a definite conclusion, but the good thing was that we were able to explain our reasoning one way or the other.

For instance with this pattern of "H"s:

The two girls were more than happy to explain their thinking:

Click on picture to see video

How about these other sequences? Do you think the first one is right? 

You can see more of this Year 4's mathematics learning on the Y4 blog.

A Square of Cubes in Year 4

It's a curious and wondrous fact that the sum of the first n cubes is the square of the nth triangular number.

For instance, with n=3, the first three cubes

 - here made in Cuisenaire rods - can be reassembled into a square:

The square is six units wide, six being the third triangle number.

The puzzle then, was to make the cubes and then make a square from them. The class managed that successfully and it might have finished there, but when the following day they were asked to create a growing pattern of their own in Cuisenaire rods

four of the girls chose to return to the square of cubes and make it bigger:

and bigger - swallowing up all the Cuisenaire rods in the school, until they had created a monster:

The next day, while the rest of the class explained their own patterns, the four girls enthused about their creation.

It was time to have a closer look at the patterns of numbers hidden inside this huge square:

square numbers

triangle numbers

And then, to round it all off, a display outside the class:

with the invitation to make the cubes and the squares from the same rods:

We rounded it all off by inviting the Year 2s and Year 3s to find out what it was all about.  The four girls explained their creation brilliantly!

Weaving the Three Times Table

This is something from the archives, from Year 1.

In our topic on clothes, we'd looked at denim under the microscope. It looked something like this:

This is the 'back' of it

We saw the way the blue threads went over two and under one. We made the pattern on a hundred square by filling the right cells white on a Word document:

Click on image to download Word doc

It looked like this when we'd finished (after correcting some mistakes):

 Then we used another Word document, printed onto A3 cartridge paper and cut with a Stanley knife along the vertical lines:

Click on image to download Word doc

On this sheet we circled the multiples of three. Now it was just a question of threading blue strips in to make the same pattern, over two numbers not circled and under the circled multiples of three. The class really concentrated and got some great results!