People normally draw factor trees like this:
This isn't right in three ways:
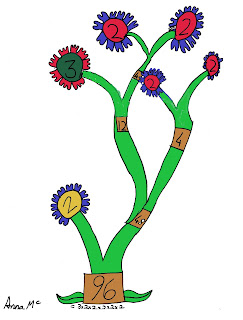
Then we drew some different factor trees to investigate the question "What different factor trees can you make for 96?" -




You can see a bigger version here.
At the same time we played a game, Ocean of Primes, adapted from the nrich Factor Track:
This isn't right in three ways:
- First of all, it should be a tree that goes up and actually looks like a tree.
- As the prime factors are so important, they should stand out.
- And - the trees should be a bit more beautiful than this.
Then we drew some different factor trees to investigate the question "What different factor trees can you make for 96?" -




Next, we thought about what mathematical questions about prime numbers we could investigate. Here are some of them:
Ella-May - Do all numbers have a two and a three as one of their prime factors?
Mr Gregg - Are there any other numbers less than 100 with six prime factors?
Sophie - Would an odd number have as many prime factors as an even number?
William - Do bigger numbers have more prime factors?
Harry - Do bigger numbers have bigger prime factors?
Some children suggested we make a huge forest of trees for lots of numbers. Here's part of it:
At the same time we played a game, Ocean of Primes, adapted from the nrich Factor Track:
To round off this term's work on factorisation we looked at a great book, Richard Evan Schwartz's You Can Count on Monsters.
In this book, all the prime numbers are monsters with particular shapes:
 |
| Two |
 |
| Three |
 |
| Five |
 |
| Seven |
Other numbers have designs made up of these ones. For instance, here's 14:
 |
| 14 has 7 and 2 as prime factors, so they're in the picture |
We had a good look at the book and the poster:
After we'd absorbed what was going on, we created some of our own in a similar style:
Each has the prime factors of the number illustrated:
 |
| Anna: 24 has the prime factors 3, 2, 2 and 2 |
 |
| Emily: 104 has 13, 2, 2 and 2 as prime factors |
 |
| Sophie: The prime factors of 144 are 3, 2, 2, 3, 2, 2 |
UPDATE - FEBRUARY 2016 - THOUGHT FLOWERS
















Mr. Gregg,
ReplyDeletePlease visit our school blog site, Newcastle, England.
We would love to hear some of your comments and we could leave you some too.
year6b.bykerblogs.net
I really like the images you have created your students. Congratulations!
ReplyDelete